1.1 为什么需要学习优化算法？

优化算法能够帮助你快速训练模型。机器学习的应用是一个高度依赖经验的过程，伴随着大量迭代的过程，你需要训练诸多模型，才能找到合适的那一个，所以，优化算法能够帮助你快速训练模型。

使用好用的优化算法能够大大提高你和团队的效率。深度学习没有在大数据领域发挥最大的效果，我们可以利用一个巨大的数据集来训练神经网络，而在巨大的数据集基础上进行训练速度很慢。因此，你会发现，使用快速的优化算法，使用好用的优化算法能够大大提高你和团队的效率.

1.2 什么是 mini-batch 梯度下降法？

在模型训练中，我们要把训练样本放到巨大的矩阵𝑋当中去，𝑋 = [𝑥(1) ，𝑥(2)， 𝑥(3) … … 𝑥(𝑚)]。

𝑌也是如此，𝑌 = [𝑦(1) 𝑦(2) 𝑦(3) … … 𝑦(𝑚)]。

所以𝑋的维数是(𝑛𝑥, 𝑚)，𝑌的维数是(1, 𝑚)，向量化能够较快地处理所有𝑚个样本。如果𝑚很大的话，处理速度仍然缓慢。比如说，如果𝑚是 500 万或 5000 万或者更大的一个数，在对整个训练集执行梯度下降法时，必须处理整个训练集，然后才能进行一步梯度下降法，然后再重新处理 500 万个训练样本，才能进行下一步梯度下降法。如果在处理完整个 500 万个样本的训练集之前，先让梯度下降法处理一部分，算法速度会更快。

你可以把训练集分割为小一点的子集训练，这些子集被取名为 mini-batch，假设每一个子集中只有 1000 个样本，那么把其中的𝑥(1)到𝑥(1000)取出来，将其称为第一个子训练集，也叫做 mini-batch，然后你再取出接下来的 1000 个样本，从𝑥(1001)到𝑥(2000)，然后再取 1000个样本，以此类推。

接下来说一个新的符号，把𝑥(1)到𝑥(1000)称为𝑋{1}，𝑥(1001)到𝑥(2000)称为𝑋{2}，如果你的训练样本一共有 500 万个，每个 mini-batch 都有 1000 个样本，也就是说，你有 5000 个mini-batch，因为 5000 乘以 1000 就是 5000 万。

你共有 5000 个 mini-batch，所以最后得到是𝑋{5000}

对𝑌也要进行相同处理，你也要相应地拆分𝑌的训练集，所以这是𝑌{1}，然后从𝑦(1001)到 𝑦(2000)，这个叫𝑌{2}，一直到𝑌{5000}。

mini-batch的数量𝑡组成了𝑋{𝑡}和𝑌{𝑡}，这就是1000个训练样本，包含相应的输入输出对。

在继续课程之前，先确定一下符号，之前我们使用了上角小括号(𝑖)表示训练集里的值，所以𝑥(𝑖)是第𝑖个训练样本。我们用了上角中括号[𝑙]来表示神经网络的层数，𝑧[𝑙]表示神经网络中第𝑙层的𝑧值，我们现在引入了大括号𝑡来代表不同的mini-batch，所以我们有𝑋{𝑡}和𝑌{𝑡}，检查一下自己是否理解无误。

𝑋{𝑡}和𝑌{𝑡}的维数：如果𝑋{1}是一个有 1000 个样本的训练集，或者说是 1000 个样本的𝑥值，所以维数应该是(𝑛𝑥,1000)，𝑋{2}的维数应该是(𝑛𝑥, 1000)，以此类推。因此所有的子集维数都是(𝑛𝑥, 1000)，而这些（𝑌{𝑡}）的维数都是(1,1000)。

解释一下这个算法的名称。

batch 梯度下降法指的是我们之前讲过的梯度下降法算法，就是同时处理整个训练集，这个名字就是来源于能够同时看到整个 batch 训练集的样本被处理。

mini-batch 梯度下降法，指的是我们每次同时处理的单个的 mini-batch 𝑋{𝑡}和𝑌{𝑡}，而不是同时处理全部的𝑋和𝑌训练集。

那么究竟 mini-batch 梯度下降法的原理是什么？在训练集上运行 mini-batch 梯度下降法，你运行 for t=1……5000，因为我们有 5000 个各有 1000 个样本的组，在 for 循环里你要做的基本就是对𝑋{𝑡}和𝑌{𝑡}执行一步梯度下降法。假设你有一个拥有1000个样本的训练集，而且假设你已经很熟悉一次性处理完的方法，你要用向量化去几乎同时处理 1000 个样本。

首先对输入也就是𝑋{𝑡}，执行前向传播，然后执行𝑧[1] = 𝑊[1]𝑋 + 𝑏[1]，之前我们这里只有，但是现在你正在处理整个训练集，你在处理第一个 mini-batch，在处理 mini-batch 时它变成了𝑋{𝑡}，即𝑧[1] = 𝑊[1]𝑋{𝑡} + 𝑏[1]，然后执行𝐴[1]𝑘 = 𝑔1，之所以用大写的𝑍是因为这是一个向量内涵，以此类推，直到𝐴[𝐿] = 𝑔𝐿，这就是你的预测值。注意这里你需要用到一个向量化的执行命令，这个向量化的执行命令，一次性处理 1000 个而不是 500 万个样本。

这是使用 mini-batch 梯度下降法训练样本的一步，也可被称为进行“一代” （1 epoch）的训练。一代这个词意味着只是一次遍历了训练集。

使用 batch 梯度下降法，一次遍历训练集只能让你做一个梯度下降，使用 mini-batch 梯度下降法，一次遍历训练集，能让你做 5000 个梯度下降。

如果你有一个训练集，mini-batch 梯度下降法比 batch 梯度下降法运行地更快，所以几乎每个研习深度学习的人在训练巨大的数据集时都会用到。

1.3 理解 mini-batch 梯度下降法（Understanding mini-batchgradient descent）

使用 batch 梯度下降法时，每次迭代都需要历遍整个训练集 ，可以预期每次迭代成本都会下降，所以如果成本函数𝐽是迭代次数的一个函数，它应该会随着每次迭代而减少，如果𝐽在某次迭代中增加了，那肯定出了问题，也许是因为学习率太大。

使用 mini-batch 梯度下降法，如果你作出成本函数在整个过程中的图，则并不是每次迭代都是下降的，特别是在每次迭代中，你要处理的是𝑋{𝑡}和𝑌{𝑡}，如果要作出成本函数𝐽{𝑡}的图，而𝐽{𝑡}只和𝑋{𝑡}，𝑌{𝑡}有关，也就是每次迭代下你都在训练不同的样本集或者说训练不同的 mini-batch，如果你要作出成本函数𝐽的图，你很可能会看到这样的结果，走向朝下，但有更多的噪声，所以如果你作出𝐽{𝑡}的图，因为在训练 mini-batch 梯度下降法时，会经过多代，你可能会看到这样的曲线（上图右部分）。

没有每次迭代都下降是不要紧的，但走势应该向下，噪声产生的原因在于也许𝑋{1}和𝑌{1}是比较容易计算的 mini-batch，因此成本会低一些。不过也许出于偶然，𝑋{2}和𝑌{2}是比较难运算的 mini-batch，或许需要一些残缺的样本，这样一来，成本会更高一些，所以才会出现这些摆动，因为是在运行 mini-batch 梯度下降法作出成本函数图。

需要决定的变量之一是 mini-batch 的大小，𝑚就是训练集的大小，极端情况下:

如果 mini-batch 的大小等于𝑚，其实就是 batch 梯度下降法，在这种极端情况下，就有了 mini-batch 𝑋{1}和𝑌{1}，并且该 mini-batch 等于整个训练集，所以把 mini-batch 大小设为𝑚可以得到 batch 梯度下降法。

另一个极端情况，假设 mini-batch 大小为 1，就有了新的算法，叫做随机梯度下降法，每个样本都是独立的 mini-batch，当你看第一个 mini-batch，也就是𝑋{1}和𝑌{1}，如果 mini-batch 大小为 1，它就是第一个训练样本。接着再看第二个 mini-batch，也就是第二个训练样本，采取梯度下降步骤，然后是第三个训练样本，以此类推，一次只处理一个。

看在两种极端下成本函数的优化情况，如果这是你想要最小化的成本函数的轮廓，最小值在中心点，batch 梯度下降法从某处开始，相对噪声低些，幅度也大一些。

相反，在随机梯度下降法中，从某一点开始，我们重新选取一个起始点，每次迭代，你只对一个样本进行梯度下降，大部分时候你向着全局最小值靠近，有时候你会远离最小值，因为那个样本恰好给你指的方向不对，因此随机梯度下降法是有很多噪声的，平均来看，它最终会靠近最小值，不过有时候也会方向错误 ，随机梯度下降法永远不会收敛，而是会一直在最小值附近波动，但它并不会在达到最小值并停留在此 。

实际上选择的 mini-batch 大小在二者之间，大小在 1 和𝑚之间，而 1 太小了，𝑚太大了，原因在于如果使用 batch 梯度下降法，mini-batch 的大小为𝑚，每个迭代需要处理大量训练样本，该算法的主要弊端在于特别是在训练样本数量巨大的时候，单次迭代耗时太长 。如果训练样本不大，batch 梯度下降法运行地很好。

相反，如果使用随机梯度下降法 ，如果你只要处理一个样本，那这个方法很好，这样做没有问题，通过减小学习率，噪声会被改善或有所减小 ，但随机梯度下降法的一大缺点是，会失去所有向量化带给你的加速 ，因为一次性只处理了一个训练样本，这样效率过于低下，所以实践中最好选择不大不小的 mini-batch 尺寸，使学习率达到最快。

合适的mini-batch会有两个好处。一方面，你得到了大量向量化 ，如果 mini-batch 大小为1000 个样本，你就可以对 1000 个样本向量化，比你一次性处理多个样本快得多。另一方面，你不需要等待整个训练集被处理完就可以开始进行后续工作 ，每次训练集允许我们采取 5000 个梯度下降步骤，所以实际上一些位于中间的 mini-batch 大小效果最好。

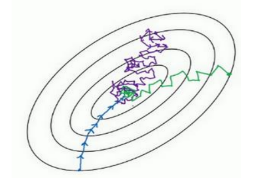
用 mini-batch 梯度下降法，从这里开始（绿线），一次迭代这样做，两次，三次，四次，它不会总朝向最小值靠近，但它比随机梯度下降要更持续地靠近最小值的方向，它也不一定在很小的范围内收敛，如果出现波动问题，可以慢慢减少学习率。

1.4 设置mini-batch的指导原则

如果 mini-batch 大小既不是 1 也不是𝑚，应该取中间值，那应该怎么选择呢？其实是有指导原则的。

首先，如果训练集较小，直接使用 batch 梯度下降法。样本集较小就没必要使用 mini-batch 梯度下降法，你可以快速处理整个训练集，所以使用 batch 梯度下降法也很好，这里的少是说小于 2000 个样本，这样比较适合使用 batch 梯度下降法。不然，样本数目较大的话，一般的 mini-batch 大小为 64 到 512，考虑到电脑内存设置和使用的方式，如果 minibatch 大小是 2 的𝑛次方，代码会运行地快一些。64 到 512 的 mini-batch 比较常见。

事实上 mini-batch 大小是另一个重要的变量，你需要做一个快速尝试，才能找到能够最有效地减少成本函数的那个，我一般会尝试几个不同的值，几个不同的 2 次方，然后看能否找到一个让梯度下降优化算法最高效的大小。希望这些能够指导你如何开始找到这一数值。

2.1 指数加权平均数的原理

有几个优化算法，它们比梯度下降法快，要理解这些算法，你需要用到指数加权平均，在统计中也叫做指数加权移动平均，我们首先学习指数加权平均，然后再来讲更复杂的优化算法。

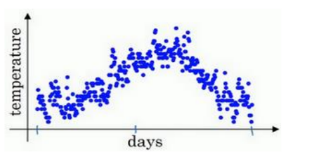
以上是一年内的气温散点图。你用数据作图，可起始日在 1 月份，中间是夏季初，尾部是年末，相当于 12 月末。

起始时间是 1 月 1 号，年中接近夏季的时候，随后就是年末的数据，看起来有些杂乱，如果要计算趋势的话，也就是温度的局部平均值，或者说移动平均值。

你要做的是，首先使𝑣0 = 0，每天，需要使用 0.9 的加权数之前的数值加上当日温度的0.1 倍，即𝑣1 = 0.9𝑣0 + 0.1𝜃1，所以这里是第一天的温度值。

第二天，又可以获得一个加权平均数，0.9 乘以之前的值加上当日的温度 0.1 倍，即𝑣2 = 0.9𝑣1 + 0.1𝜃2，以此类推。

第二天值加上第三日数据的 0.1，如此往下。大体公式就是某天的𝑣等于前一天𝑣值的 0.9加上当日温度的 0.1。

如此计算，然后用红线作图的话，便得到这样的结果。

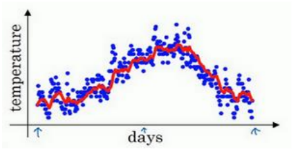
你得到了移动平均值，每日温度的指数加权平均值。

𝑣𝑡 = 0.9𝑣𝑡?1+0.1𝜃𝑡，我们把 0.9 这个常数变成𝛽，将之前的 0.1 变成(1 ? 𝛽)，即𝑣𝑡 = 𝛽𝑣𝑡?1 + (1 ? 𝛽)𝜃𝑡

由于以后我们要考虑的原因，在计算时可视𝑣𝑡大概是 1/ (1?𝛽)的每日温度，如果𝛽是 0.9，你会想，这是十天的平均值，也就是红线部分。

我们来试试别的，将𝛽设置为接近 1 的一个值，比如 0.98，计算1/(1?0.98) = 50，这就是粗略平均了一下，过去 50 天的温度，这时作图可以得到绿线。

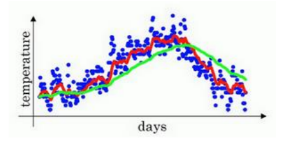
这个高值𝛽要注意几点，得到的曲线要平坦一些，原因在于多平均了几天的温度，所以这个曲线，波动更小，更加平坦，缺点是曲线进一步右移，因为现在平均的温度值更多，要平均更多的值，指数加权平均公式在温度变化时，适应地更缓慢一些，所以会出现一定延迟，因为当𝛽 = 0.98，相当于给前一天的值加了太多权重，只有 0.02 的权重给了当日的值，所以温度变化时，温度上下起伏，当𝛽 较大时，指数加权平均值适应地更缓慢一些。

我们可以再换一个值试一试，如果𝛽是另一个极端值，比如说 0.5，根据右边的公式（ 1/ (1?𝛽)），这是平均了两天的温度。

作图运行后得到黄线。

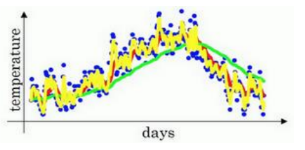
由于仅平均了两天的温度，平均的数据太少，所以得到的曲线有更多的噪声，有可能出现异常值，但是这个曲线能够更快适应温度变化。

所以指数加权平均数经常被使用。通过调整这个参数（𝛽），我们会发现这是一个很重要的参数，可以取得稍微不同的效果，往往中间有某个值效果最好，𝛽为中间值时得到的红色曲线，比起绿线和黄线更好地平均了温度。

10.2.2 指数加权平均数的本质

回忆一下这个计算指数加权平均数的关键方程。

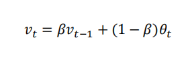
𝛽 = 0.9的时候，得到的结果是红线，如果它更接近于 1，比如 0.98，结果就是绿线，如果𝛽小一点，如果是 0.5，结果就是黄线。

我们进一步地分析，来理解如何计算出每日温度的平均值。

使𝛽 = 0.9，写下相应的几个公式，所以在执行的时候，𝑡从 0 到 1 到 2 到 3，𝑡的值在不断增加，为了更好地分析，t的顺序逆序写。

所以这是一个加和并平均，100 号数据，也就是当日温度。我们分析𝑣100的组成，也就是在一年第 100 天计算的数据，但是这个是总和，包括 100 号数据，99 号数据，97 号数据等等。画图的一个办法是，假设我们有一些日期的温度，所以这是数据，这是𝑡，所以 100 号数据有个数值，99 号数据有个数值，98 号数据等等，𝑡为 100，99，98 等等，这就是数日的温度数值。

然后我们构建一个指数衰减函数，从 0.1 开始，到0.1 × 0.9，到0.1 × (0.9)2，以此类推，这是一个指数衰减函数。

计算𝑣100是通过，把两个函数对应的元素，然后求和，用这个数值100号数据值乘以0.1，99 号数据值乘以 0.1 乘以(0.9)2，这是第二项，以此类推，所以选取的是每日温度，将其与指数衰减函数相乘，然后求和，就得到了𝑣100。

又因此当𝛽 = 0.9的时候，我们说仿佛你在计算一个指数加权平均数，只关注了过去 10天的温度，因为 10 天后，权重下降到不到当日权重的三分之一。

相反，如果，那么 0.98 需要多少次方才能达到这么小的数值？(0.98)^50大约等于1/𝑒，所以前 50 天这个数值比1/𝑒大，数值会快速衰减，所以本质上这是一个下降幅度很大的函数，可以看作平均了 50 天的温度。因为在例子中，要代入等式的左边，𝜀 = 0.02，所以1/𝜀为 50，我们由此得到公式，我们平均了大约 1 /(1?𝛽)天的温度，这里𝜀代替了1 ? 𝛽，也就是说根据一些常数，能大概知道能够平均多少日的温度，不过这只是思考的大致方向，并不是正式的数学证明。

最后讲讲如何在实际中执行，还记得吗？我们一开始将𝑣0设置为 0，然后计算第一天𝑣1，然后𝑣2，以此类推。

现在解释一下算法，可以将𝑣0，𝑣1，𝑣2等等写成明确的变量，不过在实际中执行的话，你要做的是，一开始将𝑣初始化为 0，然后在第一天使𝑣: = 𝛽𝑣 + (1 ? 𝛽)𝜃1，然后第二天，更新𝑣值，𝑣: = 𝛽𝑣 + (1 ? 𝛽)𝜃2，以此类推，有些人会把𝑣加下标，来表示𝑣是用来计算数据的指数加权平均数。

再说一次，但是换个说法，𝑣𝜃0 = 0，然后每一天，拿到第𝑡天的数据，把𝑣更新为𝑣: = 𝛽𝑣𝜃 + (1 ? 𝛽)𝜃𝑡。

10.2.3 指数加权平均的好处

指数加权平均数公式的好处之一在于，它占用极少内存，电脑内存中只占用一行数字而已，然后把最新数据代入公式，不断覆盖就可以了，正因为这个原因，它基本上只占用一行代码，计算指数加权平均数也只占用单行数字的存储和内存，当然它并不是最好的，也不是最精准的计算平均数的方法。如果你要计算移动窗，你直接算出过去 10 天的总和，过去 50 天的总和，除以 10 和 50 就好，如此往往会得到更好的估测。但缺点是，如果保存所有最近的温度数据，和过去 10 天的总和，必须占用更多的内存，执行更加复杂，计算成本也更加高昂。

所以在接下来的课程中，我们会计算多个变量的平均值，从计算和内存效率来说，这是一个有效的方法，所以在机器学习中会经常使用，更不用说只要一行代码，这也是一个优势。

10.2.4 指数加权平均的偏差修正

我们学过了如何计算指数加权平均数，有一个技术名词叫做偏差修正，可以让平均数运算更加准确，来看看它是怎么运行的。

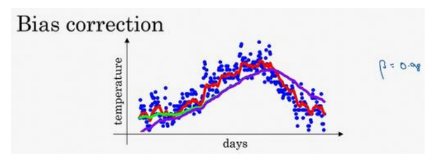
这个（红色）曲线对应𝛽的值为 0.9，这个（绿色）曲线对应的𝛽=0.98，如果你执行写在这里的公式，在𝛽等于 0.98 的时候，得到的并不是绿色曲线，而是紫色曲线，你可以注意到紫色曲线的起点较低，我们来看看怎么处理。

计算移动平均数的时候，初始化𝑣0 = 0，𝑣1 = 0.98𝑣0 +0 .02𝜃1，但是𝑣0 = 0，所以这部分没有了（0.98𝑣0），所以𝑣1 = 0.02𝜃1，所以如果一天温度是 40 华氏度，那么𝑣1 = 0.02𝜃1 = 0.02 × 40 = 8，因此得到的值会小很多，所以第一天温度的估测不准。

𝑣2 = 0.98𝑣1 +0.02𝜃2，如果代入𝑣1，然后相乘，所以𝑣2 = 0.98 × 0.02𝜃1 + 0.02𝜃2 = 0.0196𝜃1 + 0.02𝜃2，假设𝜃1和𝜃2都是正数，计算后𝑣2要远小于𝜃1和𝜃2，所以𝑣2不能很好估测出这一年前两天的温度。

了偏差。你会发现随着𝑡增加，𝛽𝑡接近于 0，所以当𝑡很大的时候，偏差修正几乎没有作用，因此当𝑡较大的时候，紫线基本和绿线重合了。不过在开始学习阶段，偏差修正可以更好预测温度，偏差修正可以使结果从紫线变成绿线。

在机器学习中，在计算指数加权平均数的大部分时候，大家不在乎执行偏差修正，因为大部分人宁愿熬过初始时期，拿到具有偏差的估测，然后继续计算下去。如果关心初始时期的偏差，在刚开始计算指数加权移动平均数的时候，偏差修正能在早期获取更好的估测。