word版本：https://download.csdn.net/download/xingghaoyuxitong/13028150

参考了《最优化计算方法及其matlab程序实现》这本书，以及前人的总结经验，在本文中主要讨论BFGS算法的相关问题，并利用此方法进行算法的求解函数的极小值。

本文目标：

1. 详细了解BFGS的推导

? ? ? ? 优化问题主流有两种方法，一是梯度下降法，一是牛顿法。牛顿法相比于梯度下降法有收敛速度快的优势，所以本文选择了牛顿法中的BFGS来进行讲解。

牛顿法的思想：

? ? ? ? 用迭代点Xk处的一阶导数（梯度）和二阶导数（Hesse阵）对目标函数进行二次函数近似，然后把二次函数的极小值点作为新的迭代点，并不断重复这一过程，直至求得满足精度的近似极小点。

对于任意一个多元函数qk(x),在Xk点进行泰勒展开获得的函数表达式为：

? ? ? ? ? ? ? ?

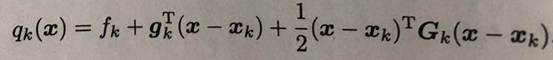
其中，gk为一阶偏导数，Gk为hesse阵

当此二次函数取极小值时，即当多元函数qk(x)的一阶导数为0时，函数取得最小值。

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?

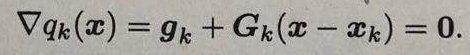
因此，牛顿法的迭代公式：

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?

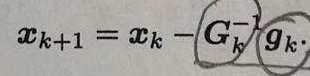
结论：到此为止，已经可以利用牛顿法来进行迭代优化操作了

1. BFGS的引入：

拟牛顿法

根据牛顿法的迭代公式可以看出，当Hesse阵不正定时，不能保证所产生的方向是目标函数在处的下降方向，特别的，当Hesse阵奇异时，算法就无法继续下去了。尽管修正牛顿法可以克服这一缺陷，但是参数Uk很难把握,等等。

拟牛顿法可以克服这些缺点。

BFGS的迭代公式：

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?

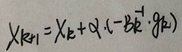
其中，Bk的更新公式为：

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?

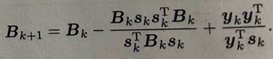
但是会发现，还是需要求解Bk的逆，这里可以引入sherman-morrism公式，求解Dk=Bk的逆

那么BFGS的迭代公式变为：

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?

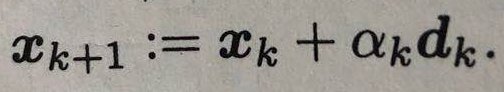
其中，

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?

? ? ? ? ? ? ? ?

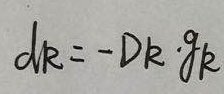
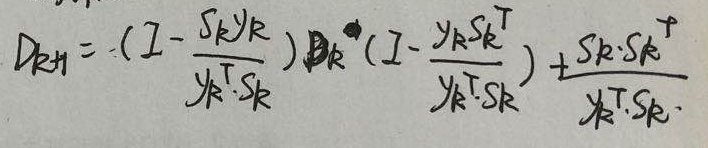
3、怎么确定ak(二分法)

目前已经确定了dk,但是还没有确定ak的值，需要使用线搜索方法线搜索方法也有很多，目前就只介绍一种，二分法

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?

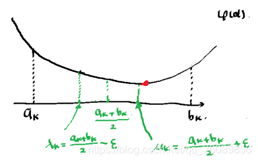
二分法是最为简单的线搜索方法，其主要思想是在给定范围内取中点，在给定的足够小的值eta左右偏移并计算
?

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?

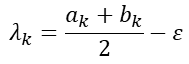
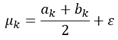
如果

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?

然后更新搜索范围。