深度学习中常用的优化算法（optimizer）_首页-傲世皇朝注册登录-连锁中心

傲世皇朝注册登录

傲世皇朝新闻 news

全国服务热线：0898-08980898

联系我们 contact us

地址：: 海南省海口市

邮箱：: admin@youweb.com

电话：: 0898-08980898

传真：: 1234-0000-5678

公司动态当前位置：首页 > 傲世皇朝新闻 > 公司动态

深度学习中常用的优化算法（optimizer）添加时间：2024-07-08

优化算法是用来求取模型的最优解的算法。

有关反向传播算法的详细推导可以参看：

小糊糊：反向传播算法详解

假设目标函数为 $J(\ heta)$ ，深度学习中的目标函数常为损失函数。深度学习中常见的损失函数参见：

小糊糊：深度学习中常用的损失函数

$\ heta$ 是模型要学习的参数， $\ abla _{\ heta}J(\ heta)$ 表示目标函数 $J(\ heta)$ 在参数 $\ heta$ 处的梯度， $\\eta$ 为学习率。

本文主要介绍梯度下降类优化算法及其变种。

批量梯度下降是先在整个数据集上计算损失函数在参数 $\ heta$ 处的梯度，然后再更新一次参数。

$\ heta=\ heta-\\eta\\cdot\ abla _{\ heta}J(\ heta)$

因为我们需要遍历整个数据集，再执行一次更新参数，所以批量梯度下降更新参数速度慢。另外批量梯度下降也不适合大数据集（内存装不下）。批量梯度下降也不适合实时场景，不能在线更新模型。但批量梯度下降的优点是训练稳定。

批量梯度下降的伪代码为：

for i in range (nb_epochs):
    params_grad = evaluate_gradient(loss_function , data , params)
    params = params - learning_rate * params_grad

随机梯度下降（SGD）每遍历一个训练数据 $(x^{(i)},y^{(i)})$ ，就计算一次梯度，更新一次参数。

$\ heta=\ heta-\\eta\\cdot\ abla _{\ heta}J(\ heta;x^{(i)};y^{(i)})$

SGD由于每次只使用一个训练数据计算梯度更新参数，所以SGD更新参数更快，模型可以在线学习。另一方面由于SGD执行频繁的更新参数，计算的梯度具有高方差，导致目标函数剧烈波动。SGD的波动性一方面可以使目标函数能够跳到更好的局部极小值，另一方面会使目标函数在最小值周围上下波动。然而，有研究表明，当我们慢慢降低学习率时，SGD显示出与批量梯度下降相同的收敛性，最后一定可以收敛到非凸优化函数的局部最小值或凸优化函数的全局最小值。

SGD的伪代码为：

for i in range(nb_epochs):
    np.random.shuffle(data)
    for example in data :
        params_grad=evaluate_gradient(loss_function , example , params)
        params=params - learning_rate * params_grad

小批量梯度下降每遍历一小批次（ $n$ 个）训练数据，更新一次参数。

$\ heta=\ heta-\\eta\\cdot\ abla _{\ heta}J(\ heta;x^{(i:i+n)};y^{(i:i+n)})$

小批量梯度下降综合了批量梯度下降和随机梯度下降（SGD）的优点，计算的梯度方差小（训练稳定），计算速度快，使用内存小。现在一般深度学习使用小批量梯度下降算法来更新模型， $n$ 常取2的指数倍。

现在常用SGD指代小批量梯度下降，下文不做特别注释SGD指小批量梯度下降。

小批量梯度下降的伪代码为：

for i in range (nb_epochs):
    np. random.shuffle (data)
    for batch in get_batches (data ,batch_size=64):
        params_grad=evaluate_gradient(loss_function , batch , params)
        params=params - learning_rate * params_grad

Momentum是一种有助于抑制SGD振荡并加快SGD向最小值收敛的方法。Momentum将过去时间的梯度向量添加到当前梯度向量。

Momentum的参数更新公式为：

$v_{t}=\\gamma v_{t-1}+\\eta\ abla _{\ heta}J(\ heta)$

$\ heta=\ heta-v_{t}$

$v_{t}$ 的计算方式类似于指数加权平均数，其中 $\\gamma$ 常取0.9。 $\\gamma$ 决定过去一段时间的梯度向量和当前时间的梯度向量的权重比。普通SGD和带Momentum的SGD训练过程对比如下图：

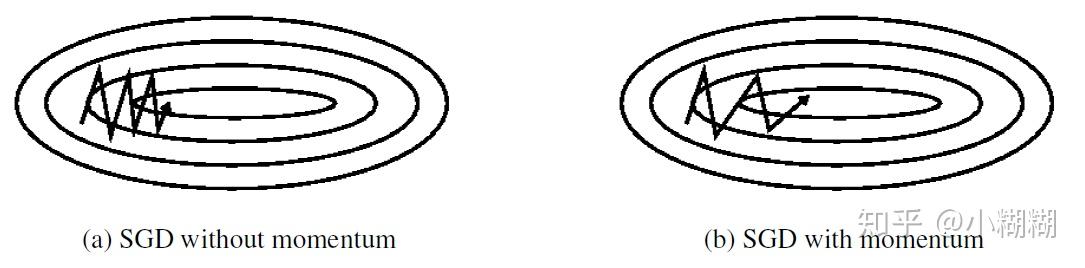
优化算法寻找目标函数最小值的过程就像使用一个小球在一个超平面滚来滚去最终滚到最低点的过程。SGD每次通过一个批次的数据决定小球接下来要滚的方向，由于每次只使用一个小批次的数据计算梯度，得到的梯度只是损失函数在这一小批次数据上的梯度。所以各个批次数据得到的梯度有一定的方差，小球每次滚的方向和距离都不一样。但是大致方向上小球还是朝着最低点前进的。如图（a）所示。

带Momentum的SGD在训练时仿佛有惯性一样，会沿着前面一段时间的梯度方向往前“冲”，就像本身具有“动量”一样。这也是Momentum名字的由来。每当小球要转变方向时，例如从“向右上”转到“向右下”，由于“动量”的存在，之前一段时间“向上”方向的动量和当前时刻“向下”方向的动量抵消，之前一段时间“向右”的动量和现在时刻“向右”的动量叠加，所以小球可以少走弯路，更快的滚向最低点。动量可以在方向错误时将其“拉”回来，方向正确时将其再“推”快点。如图（b）所示。

在前面的小球的例子中，如果小球能够事先知道自己在下一时刻的位置，那么小球就可以提前知道自己是应该“拉”回来还是“推”快点。那么小球就可以提前改变方向和速度。

NAG从这一想法出发，从Momentum的参数更新公式我们知道不管当前时刻 $\ abla _{\ heta}J(\ heta)$ 为多少， $\ heta$ 总是要先更新 $-\\gamma v_{t-1}$ 的。那么我们不妨先计算 $\ heta'=\ heta-\\gamma v_{t-1}$ ，让参数 $\ heta'$ 离下一时刻的值更近一些，让我们知道我们的参数 $\ heta$ 大概会更新到哪，我们的损失函数在下一时刻大概会到哪。然后用距离下一时刻更近的 $\ heta'$ 值来计算损失函数的值和梯度的值。

NAG的计算公式为：

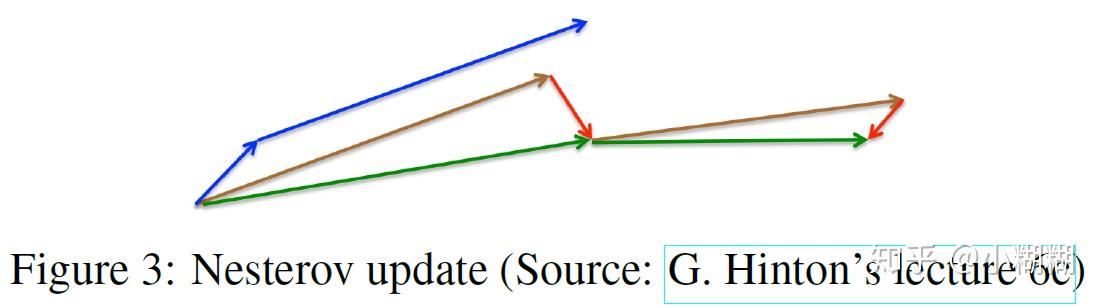
$v_{t}=\\gamma v_{t-1}+\\eta\ abla _{\ heta}J(\ heta-\\gamma v_{t-1})$

$\ heta=\ heta-v_{t}$

如下图所示，蓝色的箭头表示Momentum，左边短的蓝色箭头表示 $\\eta\ abla _{\ heta}J(\ heta)$ ，右边长的蓝色剪头表示 $\\gamma v_{t-1}$ 。棕色的箭头表示先将参数更新为 $\ heta'=\ heta-\\gamma v_{t-1}$ ，红色剪头表示 $\\eta\ abla _{\ heta}J(\ heta-\\gamma v_{t-1})$ ，绿色箭头为NAG最终优化的方向： $\\gamma v_{t-1}+\\eta\ abla _{\ heta}J(\ heta-\\gamma v_{t-1})$ 。

Adagrad在学习率 $\\eta$ 上下功夫。在每次更新参数时，对那些变化频繁的参数给与较大的学习率，变化不频繁的参数给与较小的学习率。

在之前的优化算法中，我们一次性更新所有的参数 $\ heta$ ，对每一个参数 $\ heta_{i}$ 使用同样的学习率 $\\eta$ 来更新。Adagrad在每个时间点 $t$ 对每个参数 $\ heta_{i}$ 使用不同的学习率。

令 $g_{t,i}$ 表示目标函数 $J$ 在时间点 $t$ 在参数 $\ heta_{i}$ 处的梯度，即：

$g_{t,i}=\ abla _{\ heta_{t}}J(\ heta_{t,i})$

SGD在时间点 $t$ 对参数 $\ heta_{i}$ 的更新公式为：

$\ heta_{t+1,i}=\ heta_{t,i}-\\eta\\cdot g_{t,i}$

Adagrad在时间点 $t$ 对参数 $\ heta_{i}$ 的更新公式为：

$\ heta_{t+1,i}=\ heta_{t,i}-\\frac{\\eta}{\\sqrt{G_{t,ii}+\\epsilon}}\\cdot g_{t,i}$

其中 $G_{t}$ 是一个对角矩阵，其对角线元素 $(i,i)$ 位置的值 $G_{t,ii}$ 表示从时间点0到时间点 $t$ 参数 $\ heta_{i}$ 的梯度的平方的和。 $\\epsilon$ 是防止除0的参数，常取 $1e^{-8}$ 。

那么我们可以得到Adagrad在时间点 $t$ 更新参数的向量形式：

$\ heta_{t+1}=\ heta_{t}-\\frac{\\eta}{\\sqrt{G_{t}+\\epsilon}}\\odot g_{t}$

其中 $\\odot$ 表示对应位置相乘。

Adagrad的优点是不用再手工的调整学习率。

Adagrad的缺点也很明显， $G_{t,ii}$ 是过去所有时间 $\ heta_{i}$ 的梯度的平方的聚集量，那么随着时间的推移， $G_{t,ii}$ 会越来越大，那么 $\\frac{\\eta}{\\sqrt{G_{t}+\\epsilon}}$ 会越来越小，最后趋近于0，最后导致模型的参数虽然还具有较大梯度，但是参数却无法更新。

为了解决Adagrad的缺点，Adadelta在Adagrad的基础上改进。

Adadelta使用类似于指数加权平均数来求取当前时间点的运行平均数。

目标函数在时间点 $t$ 对参数 $\ heta$ 的梯度平方的运行平均数 $E[g^{2}]_{t}$ 定义为：

$E[g^{2}]_{t}=\\gamma E[g^{2}]_{t-1}+(1-\\gamma)g_{t}^{2}$

其中 $\\gamma$ 常设为0.9。

Adagrad的参数更新方式为：

$\ heta_{t+1}=\ heta_{t}+\\Delta \ heta_{t}$

$\\Delta \ heta_{t}=-\\frac{\\eta}{\\sqrt{G_{t}+\\epsilon}}\\odot g_{t}$

先将 $G_{t}$ 替换为 $E[g^{2}]_{t}$ ，则

$\\Delta \ heta_{t}=-\\frac{\\eta}{\\sqrt{E[g^{2}]_{t}+\\epsilon}}\\cdot g_{t}=-\\frac{\\eta}{RMS[g]_{t}}\\cdot g_{t}$

作者认为如果直接使用上式更新参数， $\\Delta \ heta_{t}$ 的单位与 $\ heta$ 的单位不匹配，这样不合适。作者认为之前的SGD，Momentum，Adagrad的参数更新表达式的单位都不匹配，都不合适。作者觉得 $\\Delta \ heta_{t}$ 的单位应该和 $\ heta_{t}$ 的单位一样。例如上式中 $\ heta_{t}$ 单位是参数单位， $\\Delta \ heta_{t}$ 单位的是常数1（单位消掉了），单位都不匹配你凭啥可以直接相加？（原作者的反驳点）。

为了实现单位匹配，作者定义了如下参数更新平方值的指数加权平均数：

$E[\\Delta\ heta^{2}]_{t}=\\gamma E[\\Delta\ heta^{2}]_{t-1}+(1-\\gamma)\\Delta\ heta_{t}^{2}$

则 $RMS[\\Delta \ heta]_{t}=\\sqrt{E[\\Delta\ heta^{2}]_{t}+\\epsilon}$

因为当前时间点 $t$ 的 $RMS[\\Delta \ heta]_{t}$ 无法求得，所以我们使用上一时间点 $t-1$ 的 $RMS[\\Delta \ heta]_{t-1}$ 来近似当前时间点 $t$ 的 $RMS[\\Delta \ heta]_{t}$ 。

所以最终Adadelta的参数更新公式为：

$\\Delta \ heta_{t}=-\\frac{RMS[\\Delta \ heta]_{t-1}}{RMS[g]_{t}}\\cdot g_{t}$

$\ heta_{t+1}=\ heta_{t}+\\Delta \ heta_{t}$

这时单位匹配了， $\\Delta \ heta_{t}$ 的单位和 $\ heta_{t}$ 的单位都是参数单位。

一般将初始学习率设为1，即最开始 $\\Delta \ heta_{t}=- g_{t}$ 。

RMSprop差不多是与Adadelta同时出现的。

RMSprop和Adadelta的单位不匹配版本差不多：

$E[g^{2}]_{t}=\\gamma E[g^{2}]_{t-1}+(1-\\gamma)g_{t}^{2}$

$\ heta_{t+1}=\ heta_{t}-\\frac{\\eta}{\\sqrt{E[g^{2}]_{t}+\\epsilon}}\\cdot g_{t}$

建议 $\\gamma=0.9$ ， $\\eta=0.001$

Adam是为每一个参数计算自适应学习率的另一种算法。Adam可以看成RMSprop和Momentum的结合体。

除了像Adadelta和RMSprop一样保存过去时间的梯度平方的指数加权品均值 $v_{t}$ ，Adam还像Momentum保存了梯度的指数加权平均值 $m_{t}$ ：

$m_{t}=\\beta_{1}m_{t-1}+(1-\\beta_{1})g_{t}$

$v_{t}=\\beta_{2}v_{t-1}+(1-\\beta_{2})g_{t}^{2}$

$m_{t}$ 和 $v_{t}$ 分别是梯度的一阶矩（均值）二阶矩（无中心方差）的估计值。

由于 $m_{t}$ 和 $v_{t}$ 的初始值都设为0，即 $m_{0}=0$ ， $v_{0}=0$ 。Adam的作者发现 $m_{t}$ 和 $v_{t}$ 的值偏向于0，尤其是在训练初始时。这是因为 $\\beta_{1}$ 和 $\\beta_{2}$ 都接近1，所以 $m_{t-1}$ 和 $v_{t-1}$ 所占权重较大，导致 $m_{t}$ 和 $v_{t}$ 在初始化后很长一段时间都偏向于0。

作者通过计算经校正的一阶和二阶矩估计值来抵消这些偏差：

$\\hat m_{t}=\\frac{m_{t}}{1-\\beta_{1}^{t}}$

$\\hat v_{t}=\\frac{v_{t}}{1-\\beta_{2}^{t}}$

$\\beta_{1}^{t}$ 表示 $\\beta_{1}$ 的 $t$ 次方， $t$ 表示第 $t$ 个时间点。

最终Adam更新参数的公式为：

$\ heta_{t+1}=\ heta_{t}-\\frac{\\eta}{\\sqrt{\\hat v_{t}}+\\epsilon}\\hat m_{t}$

建议 $\\beta_{1}=0.9$ ， $\\beta_{2}=0.999$ ， $\\epsilon=10^{-8}$ 。

Adam是现在表现最好的优化算法。一般情况下用Adam算法即可。

AdaMax是Adam算法基于无穷范数（infinity norm）的变种。

令 $u_{t}=\\lim_{p \\rightarrow \\infty}{(v_{t})^{\\frac{1}{p}}}$

则AdaMax的参数更新公式为：

$u_{t}=\\beta_{2}^{\\infty}v_{t-1}+(1-\\beta_{2}^{\\infty})\\left| g_{t}\\right|^{\\infty}=max(\\beta_{2}\\cdot v_{t-1},\\left| g_{t}\\right|)$

$\ heta_{t+1}=\ heta_{t}-\\frac{\\eta}{u_{t}}\\hat m_{t}$

其中 $\\left| g_{t}\\right|^{\\infty}$ 表示 $g_{t}$ 的 $l_{\\infty}$ 范数。

由于 $u_{t}$ 依赖于max操作，所以AdaMax不像在Adam中 $m_{t}$ 和 $v_{t}$ 的偏向于0，这就是为什么我们不需要计算 $u_{t}$ 的偏差校正。比较好的默认值 $\\eta=0.002$ , $\\beta_{1}=0.9$ , $\\beta_{2}=0.999$ 。

Nadam将Adam和NAG结合。

先回忆一下momentum的参数更新规则：

$g_{t}=\ abla _{\ heta_{t}}J(\ heta_{t})$

$m_{t}=\\gamma m_{t-1}+\\eta g_{t}$

$\ heta_{t+1}=\ heta_{t}-m_{t}$

通过以上三式可得：

$\ heta_{t+1}=\ heta_{t}-(\\gamma m_{t-1}+\\eta g_{t})$ (1)

式（1）表面参数更新分为两步，先按照上一时间点 $t-1$ 的动量方向更新一步，再按照当前时间点 $t$ 的梯度方向更新一步。

NAG允许我们在计算梯度前先更新动量步参数，先预先知道未来到达的地方，用未来的梯度更新参数。

$g_{t}=\ abla _{\ heta_{t}}J(\ heta_{t}-\\gamma m_{t-1})$

$m_{t}=\\gamma m_{t-1}+\\eta g_{t}$

$\ heta_{t+1}=\ heta_{t}-m_{t}$

Nadam的作者为了将NAG融入到Adam中，提出用下面的方式向前看一步：

$g_{t}=\ abla _{\ heta_{t}}J(\ heta_{t})$

$m_{t}=\\gamma m_{t-1}+\\eta g_{t}$

$\ heta_{t+1}=\ heta_{t}-(\\gamma m_{t}+\\eta g_{t})$ (2)

逐一对比式（2）和（1），现在是用当前时刻 $t$ 的动量 $m_{t}$ 而不是上一时间点 $t-1$ 的动量来作为动部分的参数更新。相当于是在动量更新部分向前看了一步。

下面来看看如何在Adam中使用NAG：

$m_{t}=\\beta_{1}m_{t-1}+(1-\\beta_{1})g_{t}$

$\\hat m_{t}=\\frac{m_{t}}{1-\\beta_{1}^{t}}$

$\\begin{align*}\ heta_{t+1}&=\ heta_{t}-\\frac{\\eta}{\\sqrt{\\hat v_{t}}+\\epsilon}\\hat m_{t}\\\\ &=\ heta_{t}-\\frac{\\eta}{\\sqrt{\\hat v_{t}}+\\epsilon}(\\frac{\\beta_{1}m_{t-1}}{1-\\beta_{1}^{t}}+\\frac{(1-\\beta_{1})g_{t}}{1-\\beta_{1}^{t}})\\\\ \\end{align*}$

即 $\ heta_{t+1}=\ heta_{t}-\\frac{\\eta}{\\sqrt{\\hat v_{t}}+\\epsilon}(\\beta_{1}\\hat m_{t-1}+\\frac{(1-\\beta_{1})g_{t}}{1-\\beta_{1}^{t}})$ （3）

看式（3）和式（1）、（2）的结构是不是很像。

那么Nadam参数更新公式为如下，用当前时间点 $t$ 的 $\\hat m_{t}$ 代替 $\\hat m_{t-1}$ 即可，表示向前看一步。

$\ heta_{t+1}=\ heta_{t}-\\frac{\\eta}{\\sqrt{\\hat v_{t}}+\\epsilon}(\\beta_{1}\\hat m_{t}+\\frac{(1-\\beta_{1})g_{t}}{1-\\beta_{1}^{t}})$

上一篇：如何正确使用MDK-ARM优化功能，以及优化之后带来的影响

下一篇：申论名师推荐怎么写当申论遇见专家：一位备考之路的引路人

[返回列表]