算法理解：
Adam = Momentum（动量） + RMSProp（自适应） + bias correction（偏差修正）
Momentum：历史梯度的指数衰减平均
RMSProp：历史梯度平方的指数衰减平均
偏差修正：解决加权平均计算中的冷启动问题，即加权平均值的前几个与实际值相差太远。

一阶矩估计和二阶矩估计分别代表原来的动量和自适应部分。模型的梯度是一个随机变量，一阶矩表示梯度均值，二阶矩表示其方差，一阶矩来控制模型更新的方向，二阶矩控制步长(学习率)，αt/√vt 是自适应的学习率。用moveing average来对一阶矩和二阶矩进行估计。bias correct是为了缓解初始一阶矩和二阶矩初始为0带来的moving average的影响。

为什么要修正？
一方面，由于m和v的初始值为0，所以第一轮的时候会非常偏向于第2项，那么m1=0.1gt,v1=0.001gt^2, 那么m1/(√v1+?) 如果直接使用有偏估计，则有效步长亦即参数更新中的项可能大很多，需要将其修正回来，当使用偏差校正估计时：


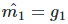
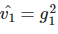
那么

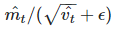
变得不那么敏感β1和β2。
另一方面，由于β1和β2非常接近1，如果不修正，对于最初的几轮迭代会有严重的影响，在训练初期mt和vt都很小，偏向于0，从而训练缓慢（β1和β2都大于0.5，很明显移动平均线偏向于初始值m0、v0），因此通过修正偏差来抵消这个倾向。

如何修正？
举个例子，因mt可以认为是梯度的平滑或近似，那么在时间步t=1：

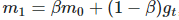
将βm0项从m1中拿出来，然后除以(1-β)，就会得到：

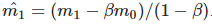
当m0=0：

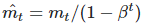
所以原理就像：乘以2（有偏差），就用除以2来“修正”它。

参考：
如何理解Adam算法
bias correction