在仿真实时环境下, 反复实验的基础上, 选取一组为实例分析并列举了多组对比实验。实验数据采用上述实验测试集, 并在仿真线程中每5 s更新一次数据。为验证算法性能, 将优化算法与A^* 算法进行了对比实验。为形象地显示实验结果, 分别以图示及评价参数表格进行对比分析。

3.3.1 实例分析算法性能

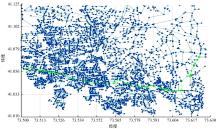
在仿真实时环境下, 以起始点100到目标节点4056为一组实例进行分析。为验证节点100~4056解的多样性, 依次得到测试集1、2、3、4、5的基于时间最短的最优路径如图4所示, 其中红、黄、白、紫、绿色路径分别表示时间测试集1、2、3、4、5下的最优路径。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 基于5个时间测试集下节点100到节点4056最优路径Fig.4 The optimal path from node 100 to node 4056 based on 5 time test sets

由图4可知:有红、黄、紫、绿4种颜色, 则说明在不同测试集下有不同的最优路径, 即节点100~4056, 在不同测试集下有4种不同的最优路径, 而图中没有白色显示, 则说明当前测试集下的最优路径与其后的最优路径重合, 即测试集3下的最优路径被测试集4、5覆盖。为进一步分析, 分别得到5个测试集的最优解如表2所示。

表2

Table 2

表2(Table 2)

表2 测试集的最优解 Table 2 The optimal solution of test set 测试集合 最优解/ms 节点数/个数 1 229 471 122 2 229 028 108 3 233 985 108 4 232 603 108 5 236 213 113

表2 测试集的最优解 Table 2 The optimal solution of test set

由表2可知:5个测试集的解均不一样, 但由图4可知, 在5个测试集下节点100~4056的最优路径仅有4条。由表中节点数可知:2、3、4测试集的节点数相同, 进一步分析, 由图4可知, 测试集3的最优路径与其后的测试集重合, 因此, 可得出测试集3与测试集4的最优路径相同, 但最优解不同。这种情况是由于实时环境下, 同一条路径下, 其值大小有所差异。

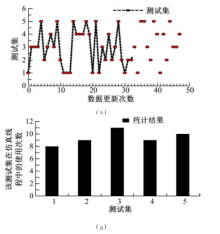
基于上述实验的基础上, 在仿真线程中, 数据一共更新47次。为简化实验并达到实验目的, 将车辆的运行时间与仿真时间之间进行了转换处理, 即运行时间1000 s等价于仿真时间的1 s。其数据随时间更新过程及测试集分布统计结果如图5所示。

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 仿真实验环境Fig.5 Simulation experiment environment

在图5(a)中, 图中实心圆点表示当前仿真数据所处的测试集中, 为更清晰显示数据随时间的变化过程, 以虚折线描述该过程。而图5(b)是对图5(a)数据分布的统计结果。

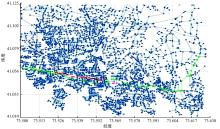
基于上述仿真环境下, 优化算法与A^* 算法的对比结果如图6、图7所示。图6是算法第一次调用A^* 算法得到的局部最优路径; 图7是在动态信息下, 调用优化算法得到的局部最优路径; 黑色矩形框为出行者行驶过的路径。

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 A* 算法的最优路径Fig.6 A* algorithm to solve the optimal path

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 本文优化算法的最优路径Fig.7 Optimization algorithm to solve the optimal path

由图6、图7可知:两图局部最优路径相同, 源于剪枝策略。当实时数据更新后, 更新局部最优解, 并以此为阈值限制算法的搜索区域。当发生剪枝时, 优化算法寻优过程结束, 则当前局部最优即为当前最优路径。为进一步验证算法的性能, 分别在运行时间、最优解、节点个数等参数上进行了对比实验, 其结果如表3所示。

表3

Table 3

表3(Table 3)

表3 对比实验结果 Table 3 The comparison of experimental results 算法 时间/ms 局部最优/ms 节点/个数 A* 26 424 229 471 122 优化 1553 228 468 119

表3 对比实验结果 Table 3 The comparison of experimental results

由表3可知:在同等测试集下, 优化算法的运行速率是A^* 算法的13倍, 甚优于A^* 算法。算法初始化时, 实时环境为初始态, 由图5可知:当前测试集为1。调用A^* 得到局部最优解, 其解值为229 471。由表2可知:测试集1下最优解值为229 471, 因此, 局部最优解与测试集1最优解相同。当黑色矩形区域行驶完成后, 所用时间为8289 s, 则当前局部最优解为221 182 s。在当前起始点下, 观察函数的返回结果为1, 调用优化算法, 得到局部最优解为228 468 s。优化算法的局部最优解大于A^* 算法, 其原于实时信息下, 导致局部最优解增大。在执行A^* 算法时实时环境为测试集1, 而由图5可知:执行优化算法时实验数据为测试集3。且由上述分析可知:在优化算法中发生剪枝, 则原路径即为测试集3下的最优路径。但测试集3下的最优解值远大于测试集1, 因此, 局部最优解增大。A^* 算法的最优路径节点个数为122, 优化算法的节点个数为119, 则两者相差3个节点, 即为图7矩形框内的节点。

3.3.2 实例分析优化策略

为验证优化策略的合理性, 针对PSO局部最优及全局最优智能存储方式以及模糊时间窗进行了实验。由于以局部最优为剪枝算法的阈值, 当观察函数检测到当前路径减少或者有折回现象时, 仅更新局部最优解而无需调用优化算法。因此, 基于局部最优优化策略下, 算法的运行时间均在4 ms左右, 运行速率明显优于优化算法。因此, 在混合优化算法中引入局部最优是有效的。

全局最优解是一个逐步求解的过程, 全局最优解随起始点变化而变化, 直到到达目标节点。基于上述求解过程, 全局最优解为233 836 s。在仿真线程中, 数据更新了47次, 则47× 5 s× 1000=235 000 s接近于车辆行驶时间23 2300 s, 因此, 模糊时间窗在控制仿真时间是有效的。由表3可知:1、2测试集最优解优于全局最优, 而3、4、5劣于全局最优。进一步结合测试集分布情况可知:测试集1、2共执行了17次, 则3、4、5测试集共执行了30次。由此可见, 全局最优解是有效的, 全局最优路径如图8所示。

图8

Fig.8

	Figure Option ViewDownloadNew Window
	图8 全局最优路径Fig.8 Global optimal path

3.3.3 多组对比实验

为进一步验证算法的性能, 列举10组对比实验, 且每组实验测试20次求均值, 统计结果如表4所示。

表4

Table 4

表4(Table 4)

表4 10组20次实验均值统计结果 Table 4 Statistical results of 20 experiments in 10 groups 序号 起始节 点编号 目标节 点编号 A* 算法 /ms 优化算法 /ms 优化策 略/ms 1 3914 3582 10900.1 109.5 1.4 2 800 1890 23417.2 1613.7 4.2 3 645 3678 15378.3 12593.6 3.3 4 394 3340 32087.4 1 2.2 5 1808 2622 6193.8 3655.5 2.9 6 929 3705 23989.1 17872.5 3.8 7 2184 4041 16856.2 11282.4 3.6 8 1750 3694 14196 1517.6 2.6 9 1711 3715 14050.1 10703.6 3.8 10 1544 2304 6005.5 2163.2 1.6

表4 10组20次实验均值统计结果 Table 4 Statistical results of 20 experiments in 10 groups

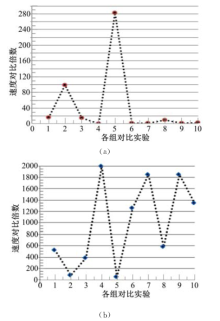
10组对比结果统计如图9所示, 图9(a)为A^* 算法与优化算法运算速率比值统计结果, 图9(b)为优化算法与优化算法中引入优化策略的运算速率比值的统计结果。

图9

Fig.9

	Figure Option ViewDownloadNew Window
	图9 对比实验统计结果Fig.9 The contrastive experiment result

由图9可知:优化算法的运算速率均优于A^* 算法, 比值分布在不同区间。由于算法是基于广义自适应A^* 算法的基础上结合剪枝算法的优化算法, A^* 算法中以优先队列Q存储待扩展节点, 并以剪枝阈值为结束条件之一, 进而加快算法运算速率。相比优化算法与优化策略速率比值可知:引入优化策略后, 算法运行速率均甚优于优化算法, 原于优化策略适应于实时环境。基于上述优化策略, 在观察函数中, 判断当前起始点S_start下的w_ij是否发生变化:当w_ij减小且发生在局部最优解, 则无需调用优化算法重构最优路径, 仅需修改P_local值, 因此节省大量运行时间; 当w_ij未发生变化, 同样, 无需调用优化算法, 等待仿真线程更新数据。因此, 优化策略可有效避免调用优化算法, 提高算法运行效率, 从而更好的适应动态实时环境。因此, 进一步证明了优化策略的有效性。