神经网络优化器对比

待优化参数w,损失函数loss,学习率lr，每次迭代一个batch，，每次迭代一个batch,t表示当前batch迭代的总次数。

1、 计算t时刻损失函数关于当前参数的梯度 

 

 

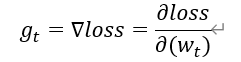
2、 计算t时刻一阶动量  和二阶动量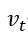

3、 计算t时刻下降梯度：

 

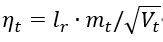
4、 计算t+1时刻参数：

 

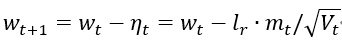
一阶动量：与梯度相关的函数

二阶动量：与梯度平方相关的函数

不同的优化器实际上只是定义了不同的一阶动量和二阶动量公式。

 

SGD(随机梯度下降)无momentum,常用的梯度下降法

 

 

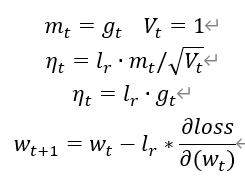
SGDM(含momentum的SGD),在SGD基础上增加一阶动量。

 

 

 

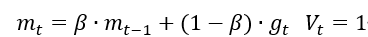
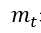表示各时刻梯度方向的指数滑动平均值。

 

 

 

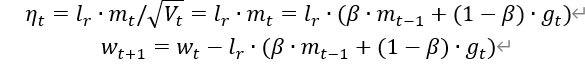
0时刻m_w, m_b=0 , 0

Beta=0.9 #超参数

# SGD-Momentun

 

 

 

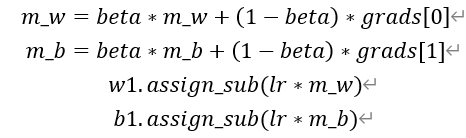
Adagrad,在SGD基础上增加二阶动量

 

 

 

 

 

 

 

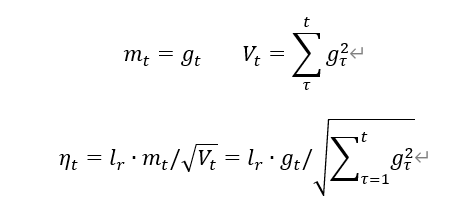
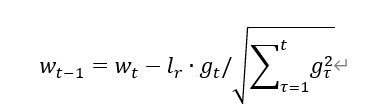
Adagrad

 

 

 

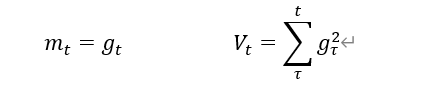
v_w ,v_b=0,0

# adagrad

v_w +=tf.square(grads[0])

v_b +=tf.square(grads[1])

w1.assign_sub(lr*grads[0]/tf.sqrt(v_w))

b1.assign_sub(lr*grads[1]/tf.sqrt(v_b))

 

RMSProp，SGD基础上增加二阶动量

 

 

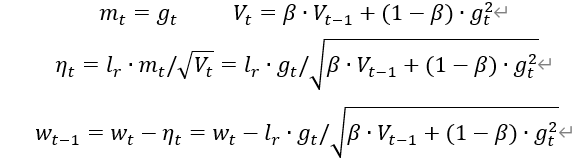
RMSProp

 

 

 

 

##

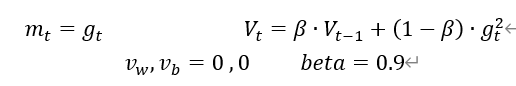
v_w=beta * v_w + (1-beta)*tf.square(grads[0])

v_b=beta * v_b + (1-beta)*tf.square(grads[1])

w1.assign_sub(lr * grads[0] / tf.sqrt(v_w))

b1.assign_sub(lr * grads[1] / tf.sqrt(v_b))

 

Adam,

同时结合SGDM一阶和RMSProp二阶动量

 

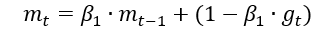
修正一阶动量的偏差：

 

 

 

 

 

 

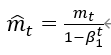
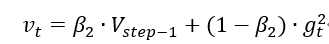
 修正二阶动量的偏差：

 

 

 

 

 

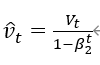
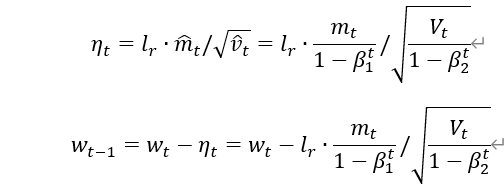
Adam

m_w , m_b=0 , 0

v_w, v_b=0, 0

beta1,beta2=0.9 ,0.999

delta_w,delta_b=0, 0

global_step=0

m_w=beta1 * m_w + (1-beta1) * grads[0]

m_b=beta1 * m_b + (1-beta1) * grads[1]

v_w=beta2 * v_w + (1-beta2) * tf.square(grads[0])

v_b=beta2 * v_b + (1-beta2) * tf.square(grads[1])

 

m_w_correction=m_w / (1-tf.pow(beta1,int(global_step)))

m_b_correction=m_b / (1-tf.pow(beta1,int(global_step)))

v_w_correction=v_w / (1-tf.pow(beta2,int(global_step))

v_b_correction=v_b / (1-tf.pow(beta2,int(global_step))

 

w1.assign_sub(lr * m_w_correction / tf.sqrt(v_w_correction)

b1.assign_sub(lr * m_b_correction / tf.sqrt(v_b_correction)

 

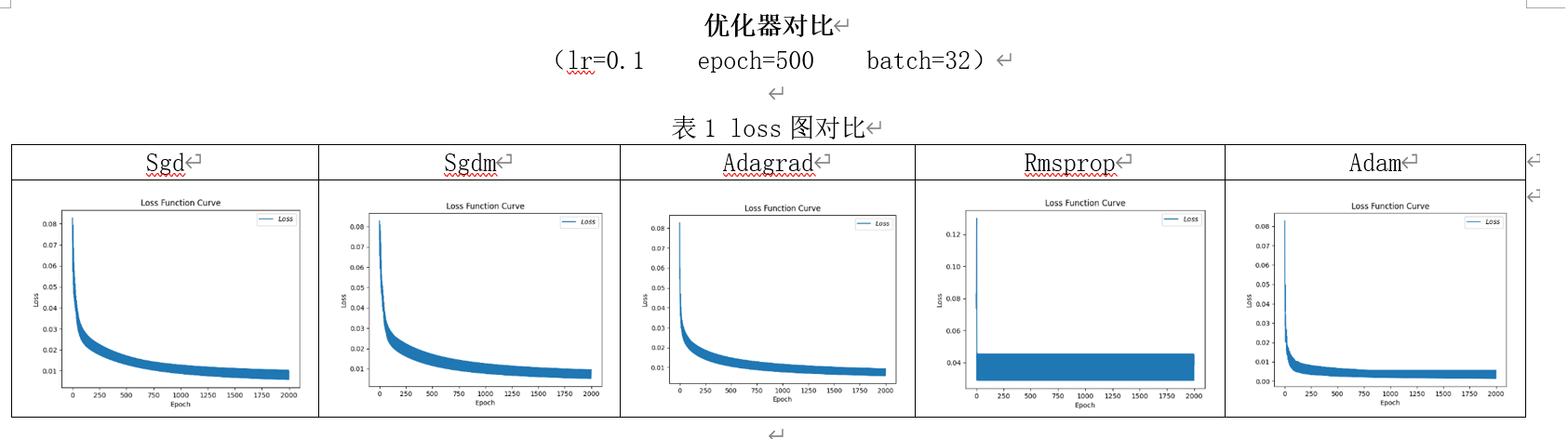
 各优化器 loss 图对比

 

 

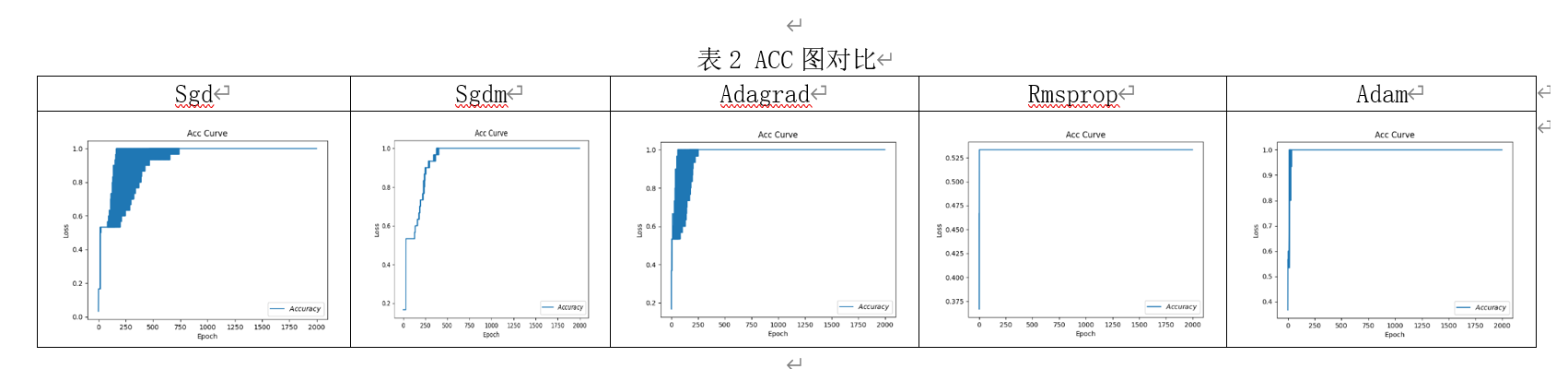
 ACC 图对比

 

 训练耗时