目录

一、粒子群优化算法（Particle Swarm Optimization，PSO）

二、多目标优化&Pareto支配

三、多目标粒子群优化算法（Multiple Objective Particle Swarm Optimization，MOPSO）

四、参考文献：

---

粒子群算法(PSO)[1]是一种群智能优化算法，于1995年Kennedy和Eberhart提出，其灵感来源于鸟群的协作觅食行为。在PSO中，每只鸟被抽象为一个粒子，其觅食行为被抽象为寻优过程。

每个粒子都有属于自己位置和飞行速度，粒子的位置是优化问题的决策变量，飞行速度则由该粒子迄今为止搜索到的最优解pBest和所有粒子的搜索到的最优解gBest共同决定，飞行速度的计算过程体现了鸟群的协作觅食。

第i个粒子的速度和位置的更新公式如下：

速度更新：

位置更新：

其中，是惯性权重系数，是对先前速度的记忆项。和是学习因子，是该粒子的当前位置和该粒子的历史最优位置之间的一个矢量，可以认为是自我认知项。是粒子的当前位置和所有粒子搜寻到的最优位置之间的一个矢量，可以认为是群体认知项。这三项共同作用更新粒子i的速度和位置。

举个简单的例子：

比如我们想要最小化下面这个目标函数（一般都是最小化）：

假设粒子i的当前位置为，上次速度为，历史最优位置。全体粒子的最优位置，，，惯性权重系数。

由速度更新公式得

?

由位置更新公式得

?

更新位置前的目标函数值，更新位置后的目标函数值，对比更新位置前后的目标函数值，可以发现目标函数值显著降低。不断更新种群中所有粒子的速度和位置，达到最大迭代次数后退出，输出最优解，即完成了粒子群优化过程。

---

在上面的例子中，预优化的目标函数只有一个，这类优化称为单目标优化。在实际应用中，往往有多个目标函数（一般是2个或3个），这类优化一般称为多目标优化（Multiple Objective Optimization or Multiobjective Optimization），多目标优化要做的就是同时优化（最小化）这两个目标函数。在单目标优化中，两个解谁更优是很明显的，目标函数更小的解即是更优解。但是在多目标优化中，两个解谁更优就没那么好判断了。

在下图中，S1明显比S2更优，因为解S1的两个目标函数值都比解S2的两个目标函数值小。

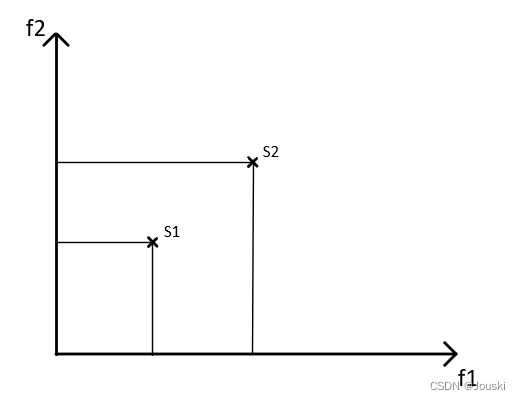
?我们来看另一种情况，对于f1，解S1比S2小，对于f2，解S2比S1小，这时候存在更优解吗？答案是否定的，在这种情况下，不存在谁比谁更优的说法，这两个解都是最优解。所以我们说，对于多目标优化，通常不存在单个最优解，而是存在一系列最优解。?

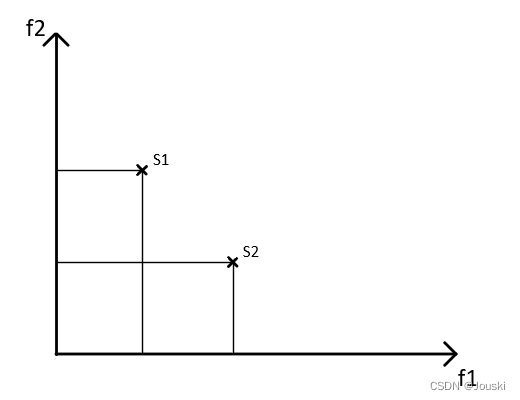
讨论两个目标函数f1和f2的多目标优化问题，现有两个解S1和S2。如果S1的两个目标函数值都比S2的两个目标函数值小，那么解S1支配解S2，如第一幅图所示；如果S1的目标函数值一个比S2的目标函数值小，一个比S2的目标函数值大，那么解S1和解S2互不支配，如第二幅图所示。

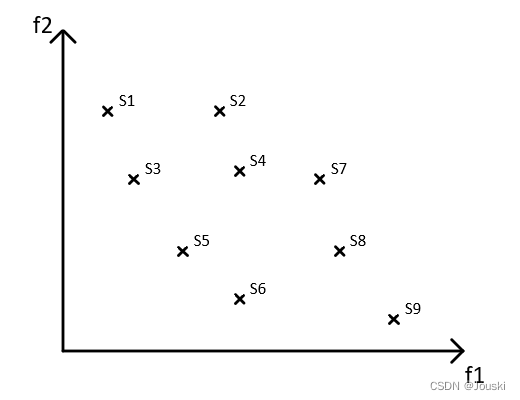
在下图中，解S1、S3、S5、S6、S9互不支配且不被其他解支配，这五个解称为Pareto解或非支配解。在下图的多目标优化问题中，如果在整个可行的变量空间中再不能找到解能够支配上述五个解，那么上述五个解称为Pareto最优解，所有的Pareto最优解组成Pareto最优解集。

在参考文献[2]中，对多目标优化问题中的支配关系有更专业的数学描述，如下：

---

多目标粒子群算法由Coello Coello等人于2002年提出（网上很多文章说是2004年提出的，但我能找到的最早论文是2002年，详见参考文献[3]）。MOPSO的粒子速度和位置的更新公式如下：

速度更新公式：

位置更新公式：

对比PSO的更新公式，可以发现MOPSO大体上和PSO类似。事实上这两个优化算法的主要的不同是在pBest和gBest的选取上。

pBest的选取：在PSO中，粒子i的pBest是粒子i迄今为止搜索到的最优位置。若更新位置后的粒子的目标函数值比这个粒子的pBest的目标函数值小（粒子比它的pBest更优），则令粒子的pBest为粒子当前的位置。但是在MOPSO中，由于多个目标函数的存在，使得粒子和它的pBest谁更优变得不好判断。所以在MOPSO中引入了Pareto支配的概念，若粒子i支配它的pBest，则粒子i最新的pBest为当前粒子i；若粒子i和它的pBest互不支配，则随机选择某一个作为最新的pBest。在参考文献[2]中，对此的描述如下：

论文片段大意：当粒子的当前位置优于其记忆中包含的位置时，使用下列公式更新粒子的位置：。决定记忆中保留什么位置的标准是利用Pareto支配（即如果记忆中的位置支配当前位置时，则保留记忆中的位置；否则当前位置取代记忆中的位置；如果他们互不支配，则随机选择其中一个）。

gBest的选取：在速度更新公式中，可以看到原先的gBest变成了REP[h]。MOPSO中定义了一个REP（repository），它是一个外部储存库，用于储存搜索过程中发现的非支配粒子。所以算法要做的其实就是在REP中选一个粒子来作为gBest，这个过程其实就是在确定REP的索引h的值。

在参考文献[3]中对确定h值的过程的描述如下：

论文片段大意：索引h值的选择过程如下：这些包含多个粒子的超立方体的适应度等于任意数字x>1（我们在实验中使用的x=10）除以它们包含的粒子数量的值。它的目的是减少那些包含多个粒子的超立方体的适应度，它可以认为是共享适应度的一种形式。然后我们将这些适应度值应用于轮盘赌来选择超立方体，再选择相应粒子。当选中某个超立方体后，我们随机选择超立方体中的一个粒子。

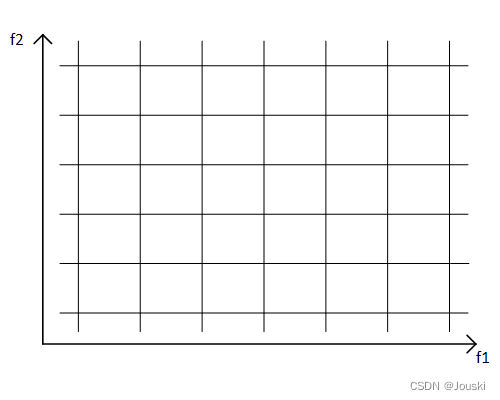
论文中的超立方体（hypercube）在我看来就是网格。其实就是将目标空间划分成一个个网格，类似于下图的处理方法。划分网格后，就能知道每个网格中有几个粒子，同理也就能知道某个粒子在哪个网格中，方便后续处理。

不知道各位大佬们有没有看懂论文是怎么确定h值的，反正我看的不是很懂。看了好几遍，最后还是看了PlatEMO[4]的MOPSO代码才看懂是怎么确定h值的。

个人的理解大概是这样的：假设现在的REP中有好些个粒子，如下图。

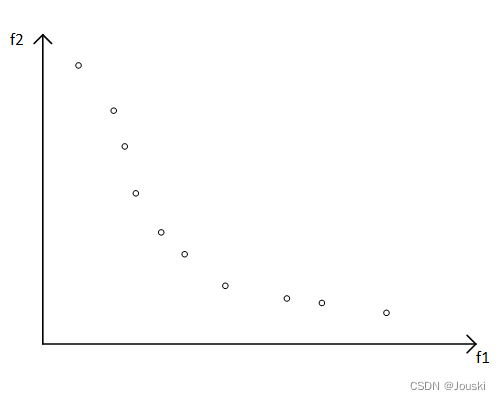
生成（在本例中生成，生成几乘几由使用者决定）的网格，网格的顶点由这些粒子在各个目标函数上的极大值和极小值确定。为方便表述，我们给有粒子的网格标上序号1~7。在所有标有序号的网格中，有的网格有一个粒子（2、3、5、7），有的网格有两个粒子（1、4、6）。

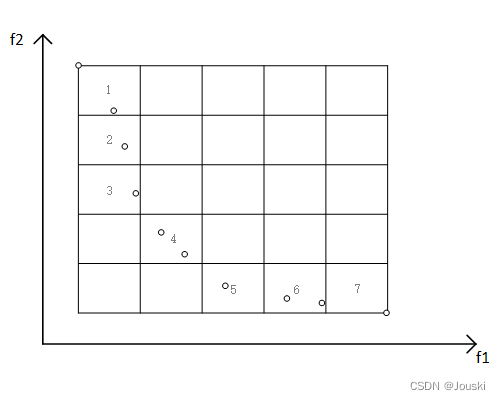
网格1~7中的粒子数目分别为：2、1、1、2、1、2、1，将这些值作为适应度值进行轮盘赌选择法（在PlatEMO的轮盘赌选择函数中，会将输入进来的适应度值求倒数，更小的适应度值有更大的概率被选中，这一点跟很多文章的轮盘赌选择不一样），来选择网格，如下图所示。

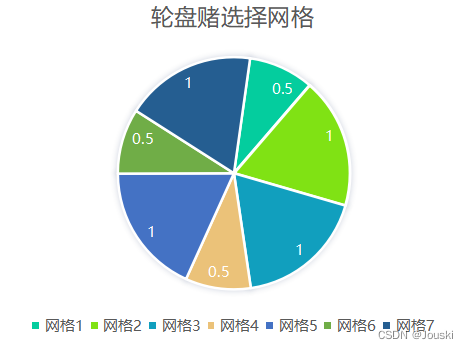
在选定网格后，随机选择一个该网格中的粒子，根据这个粒子确定h值。比如轮盘赌选到了网格2，网格2中只有一个粒子，所以只能选择该粒子，我们假设这个粒子是REP中的第3个粒子，故h=3，这样就完成确定索引h值的过程。

将REP[h]作为所谓gBest，即可完成粒子的速度更新，整个多目标粒子群算法就可以完整运行了。

---

MOPSO的作者Carlos A. Coello Coello在2004年发表了另一篇paper阐述MOPSO：Handling multiple objectives with particle swarm optimization（详见参考文献[5]），其中对REP有一段更详细的描述，如下所示。不做解读，翻译也仅可供参考。

论文片段大意：B.外部储存库：外部储存库（或者叫归档集）的主要目的是保存在搜索过程中发现的非支配向量的历史记录。这个外部储存库主要包含两部分：归档集控制器（the archive controller）和网格（the grid）。

对归档集控制器（the archive controller）的描述如下：

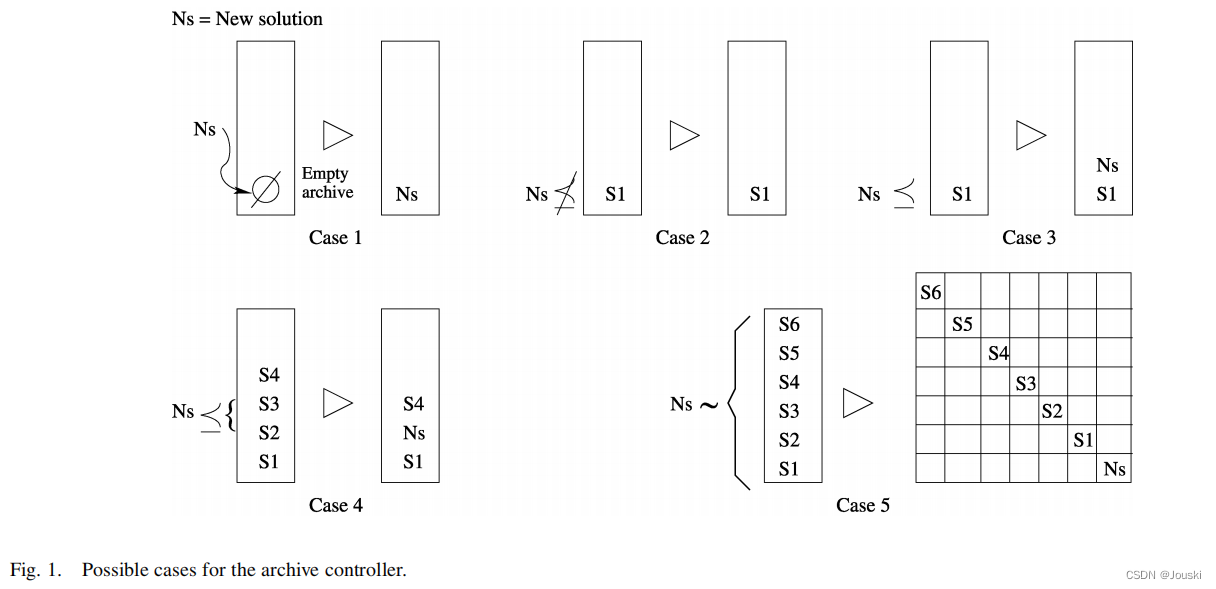
论文片段大意：1）归档集控制器：归档集控制器的功能是决定一个解是否能被添加到归档集中。决策过程如下。算法的种群每次迭代发现的非支配向量与外部储存库的向量进行比较，这个外部储存库在一开始的时候是空的。如果外部的归档集是空的，则接受当前解（见Fig1，case1）。如果这个新解被外部归档集中的某个个体支配，则新解将自动被移除（见Fig1，case2）。否则如果外部归档集中的个体没有一个支配想进入归档集的解，则这个解将被存储在外部归档集中。如果归档集中存在某些解被新解支配，则这些解将从归档集中移除（见Fig1，case3、4）。最后，如果外部种群达到最大容量，则启动自适应网格程序（见Fig1，case5）。

Fig1：

对网格（the grid）的描述如下：

论文片段大意：?2）为了获得均匀分布的Pareto前沿，我们的方法使用了[21]中提出的自适应网格技术。其基本思想是使用一个外部归档集储存所有非支配解。在归档集中，目标函数空间被分割成几个区域，如Fig2所示。注意，如果外部种群中的个体在当前网格边界外，则必须重新计算网格并且重新定位网格中的每个个体（见Fig3）。

Fig2：

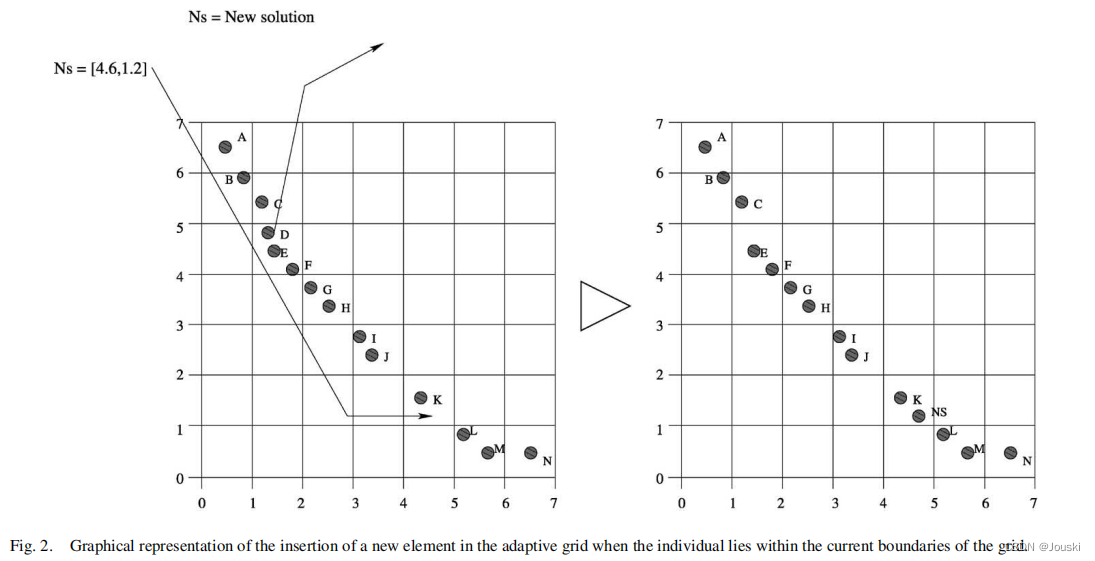
?Fig3：

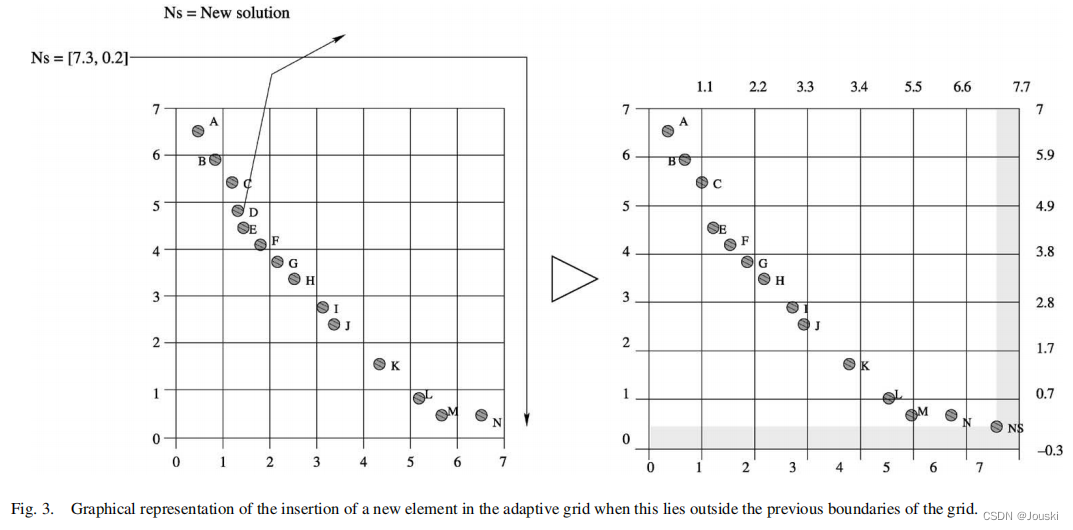
论文片段大意：自适应网格实际上是一个超立方体形成的空间。这个超立方体的维度和目标函数一样多。每个超立方体可以被解释为一个不含任何个体的地理区域。自适应网格技术的主要优点是其计算开销少于小生境技术（复杂度的分析详见[21]）。唯一的例外是如果网格在每一代都必须更新。此时，自适应网格技术的计算复杂度和小生境技术的计算复杂度相同（即）。自适应网格用于实现解的均匀分布。为了实现这个目标，有必要提供确定的信息（即子网格的数量）。

---

[1]、Kennedy J, Eberhart R. Particle swarm optimization[C]//Proceedings of ICNN'95-international conference on neural networks. IEEE, 1995, 4: 1942-1948.

[2]、郑金华. 多目标进化算法及其应用[M]. 科学出版社, 2007.

[3]、Coello C A C, Lechuga M S. MOPSO: A proposal for multiple objective particle swarm optimization[C]//Proceedings of the 2002 Congress on Evolutionary Computation. CEC'02 (Cat. No. 02TH8600). IEEE, 2002, 2: 1051-1056.

[4]、Tian Y, Cheng R, Zhang X, et al. PlatEMO: A MATLAB platform for evolutionary multi-objective optimization [educational forum][J]. IEEE Computational Intelligence Magazine, 2017, 12(4): 73-87.

[5]、Coello C A C, Pulido G T, Lechuga M S. Handling multiple objectives with particle swarm optimization[J]. IEEE Transactions on evolutionary computation, 2004, 8(3): 256-279.